Laurent Series for 1/(e^z - 1)
Source of the problem
Basic Complex Analysis 3rd Edition by Jerrold E. Marsden and Michael J. Hoffman (1999). Exercise #11 on page 236.
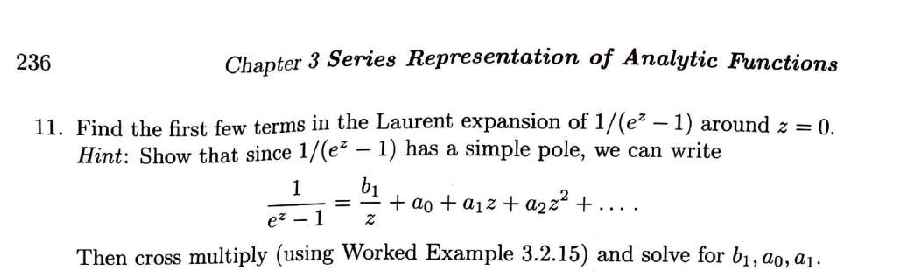
Solution
To find the Laurent series expansion of \(\frac{1}{e^z - 1}\) around \(z = 0\), we start by expressing \(e^z - 1\) as a power series. We know that:
\(e^z - 1 = \sum_{n=1}^{\infty} \frac{z^n}{n!}\)
The Laurent series for \(\frac{1}{e^z - 1}\) with undetermined coefficients is:
\(\frac{1}{e^z - 1} = \frac{b_1}{z} + a_0 + a_1z + a_2z^2 + \ldots\)
To find the coefficients, we multiply the two series and set the product equal to 1:
\[\begin{align*} \frac{1}{e^z - 1} \cdot (e^z - 1) &= \left( \frac{b*1}{z} + a_0 + a_1z + a_2z^2 + \ldots \right) \left( \sum*{n=1}^{\infty} \frac{z^n}{n!} \right) \\ &= b_1 + (\frac{b_1}{2} + a_0)z + (\frac{b_1}{6} + \frac{a_0}{2} + a_1)z^2 + \ldots \\ &= 1 \end{align*}\]
By equating the coefficients of the powers of \(z\) on both sides of the equation, we get a system of equations:
- The coefficient of \(\frac{1}{z}\) gives us \(b_1 = 1\).
- The constant term gives us \(\frac{b_1}{2} + a_0 = 0\).
- And so on for the higher powers of \(z\).
Solving these equations sequentially will give us the values of \(b_1\), \(a_0\), \(a_1\), etc.
For example:
\(b_1 = 1\)
\(\frac{b_1}{2} + a_0 = 0 \implies a_0 = -\frac{1}{2}\)
And you would continue this process to solve for \(a_1\), \(a_2\), and so on.