Introduction to Quotient Spaces in Topology

This blog is part of a series designed to demystify various concepts within the realm of linear algebra and topology. Following our discussion on vectors, we will now turn our attention to quotient spaces — a fundamental concept in topological study.

Ayumu's lecture provides an accessible approach to explaining quotient-related topics in topology. This blog aims to continue that tradition, ensuring that complex ideas are broken down into comprehensible, bite-sized pieces for anyone interested in this fascinating aspect of mathematics.

Quotient Spaces Simplified

I encountered this concept while delving into topological manifolds, and here's a simplified explanation.

Quotienting: A Primer

Generally speaking, 'quotienting' is the process of categorizing, classifying, or dividing. A familiar example from primary school is the division of natural numbers. For instance, if we have 8 apples and wish to distribute them equally among 4 people, we perform the operation \(8 \div 4\), yielding 2. This result is known as the quotient. But what does this really mean?

Consider a group of apples, with specific colors allocated to each person:

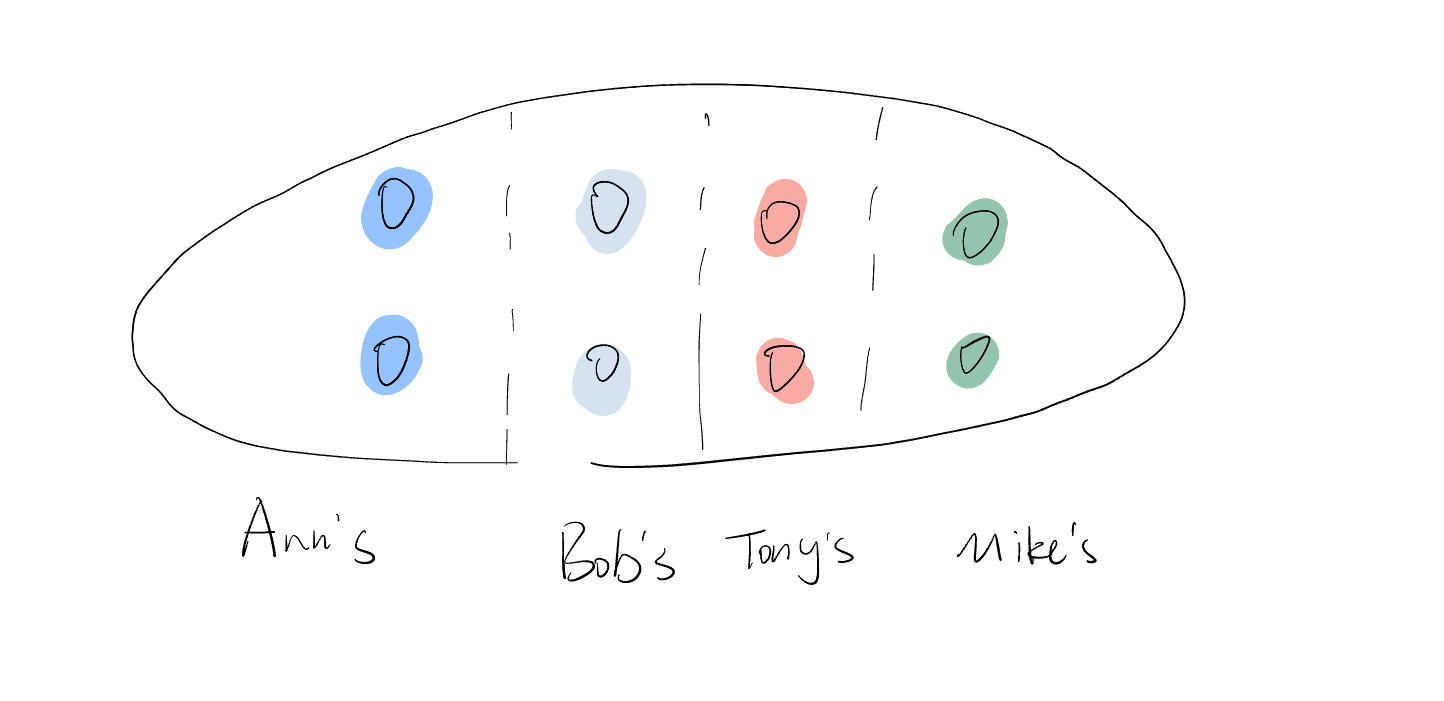
• Blue apples are given to Ann.
• Gray apples are given to Bob.
• Red apples are given to Tony.
• Green apples are given to Mike.

In this case, we have categorized or classified or divided the 8 apples. We can clear see that we devided 8 apples into 4 classes, each of which has 2 apples.

Understanding the Quotient Topology

Let's extend this concept to a topological space. Given a topological space \((X, \tau)\), we can similarly categorize or divide the space. This process involves :

1. Defining an equivalence relation on \(X\).
2. This relation partitions \(X\) into equivalence classes.
3. These classes can be viewed as a division of \(X\).
4. This partitioning results in the quotient set \(X/_\sim\).
5. There is a canonical projection (or natural map) from \(X\) to \(X/_\sim\).
6. A surjection followes.

Once one of these elements is established, the others follow naturally. Thus, there is no order of which happens and which followes, they live togethor, die together.

The Interconnectedness of Quotient Concepts

Let's discuss how the first five concepts occur together. This is relatively straightforward. Then, we will examine how the fifth concept leads to the sixth. The next section will focus on the reverse: how the sixth concept informs the first five.

Consider an equivalence relation \(\sim\) (which is reflexive, transitive, and symmetric) on a set \(X\). This partitions \(X\) into equivalence classes, such that:

\[X/_\sim = \{[x] : x \in X\}, \quad \text{where} \quad [x] = \{y \in X : y \sim x\}.\]

It's evident that the empty set is not a part of \(X/_\sim\). Moreover, these equivalence classes are mutually exclusive and their union constitutes \(X\). Thus, we have effectively partitioned \(X\).

The resulting partition \(X/_\sim\) is termed the quotient set. Accompanying this set, there is a natural or canonical projection that maps each element \(x\) in \(X\) to its equivalence class \([x]\) (denoted \(x \mapsto [x]\)).

This mapping is easily verified as a surjection, which guarantees that every equivalence class in \(X/_\sim\) has at least one preimage in \(X\), since no equivalence class is empty.

From Surjection to Equivalence Classes

Surjection implies the existence of equivalence classes, partitioning of the set, and deciding a canonical projection. If we assume a surjection \(f: X \to Y\) where \(f(x) = y\), we know that for each \(y\) in \(Y\), the preimage \(f^{-1}(y)\) is non-empty. This preimage can serve as an equivalence class.

If we define an equivalence relation \(\sim\) such that \(a \sim b\) if \(f(a) = f(b)\), then we discover the equivalence classes \(\{[x]: f^{-1}(y) \, \text{for} \, f(x) = y\}\).

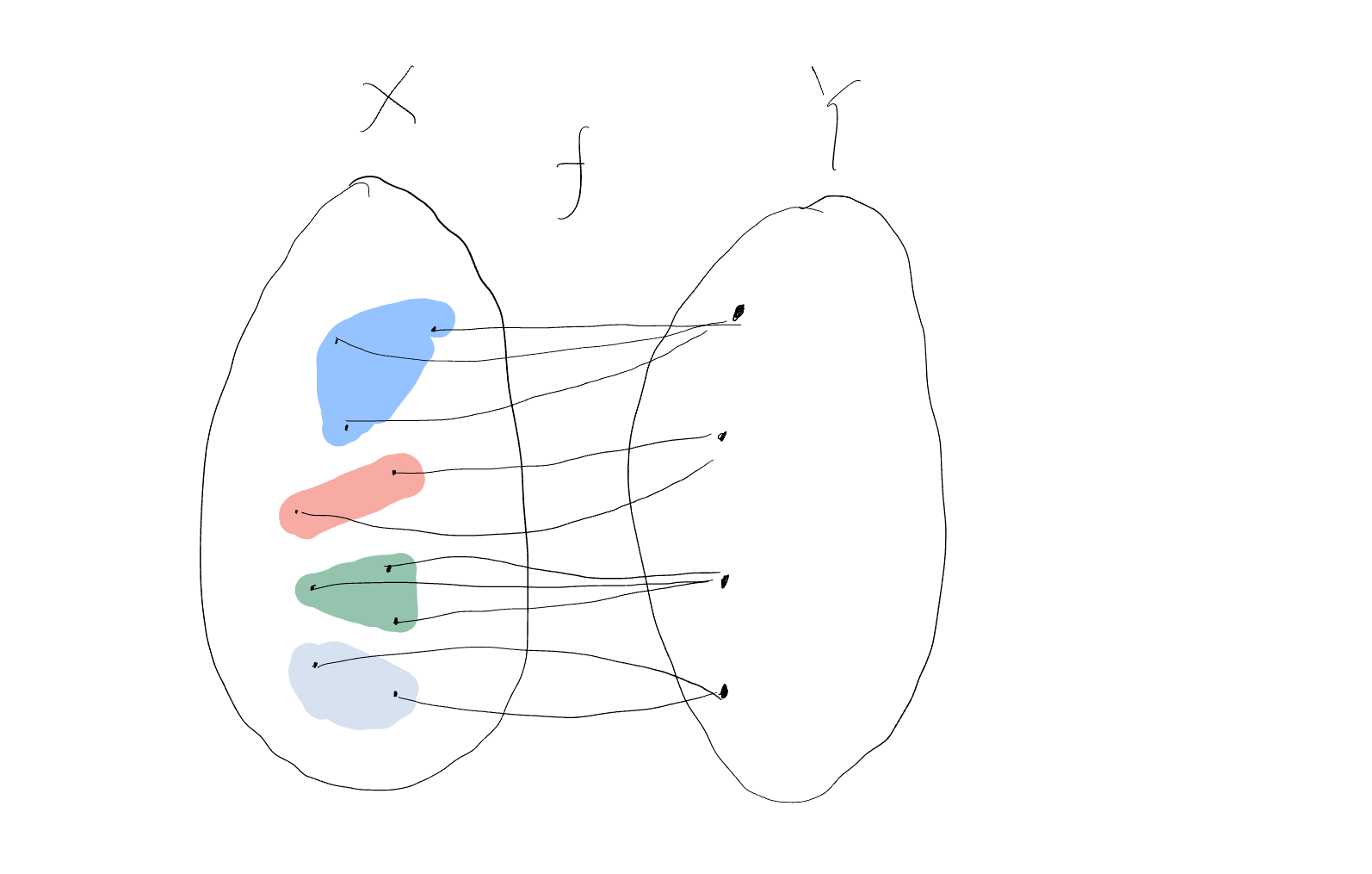
This allows us to observe that the set \(\{f^{-1}(y): y \in Y\}\) is effectively the quotient set \(X/_\sim\) ( that is, \(Y \cong X/_\sim\)) as each \(y\) in \(Y\) corresponds uniquely to an equivalence class in \(X\), establishing a bijection between \(Y\) and \(X/_\sim\).

In our next blog, we will explore further into the nuances of quotient spaces and their applications. Join us as we continue to unpack the layered concepts of topology in a way that is accessible and engaging.