Metric in L^p

This is a note for proof of

\[ \left[ \int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx\right]^{\frac{1}{p}} \]

is a norm of \(L^p\) space. Here is the structure of the whole proof (separated into different blogs):

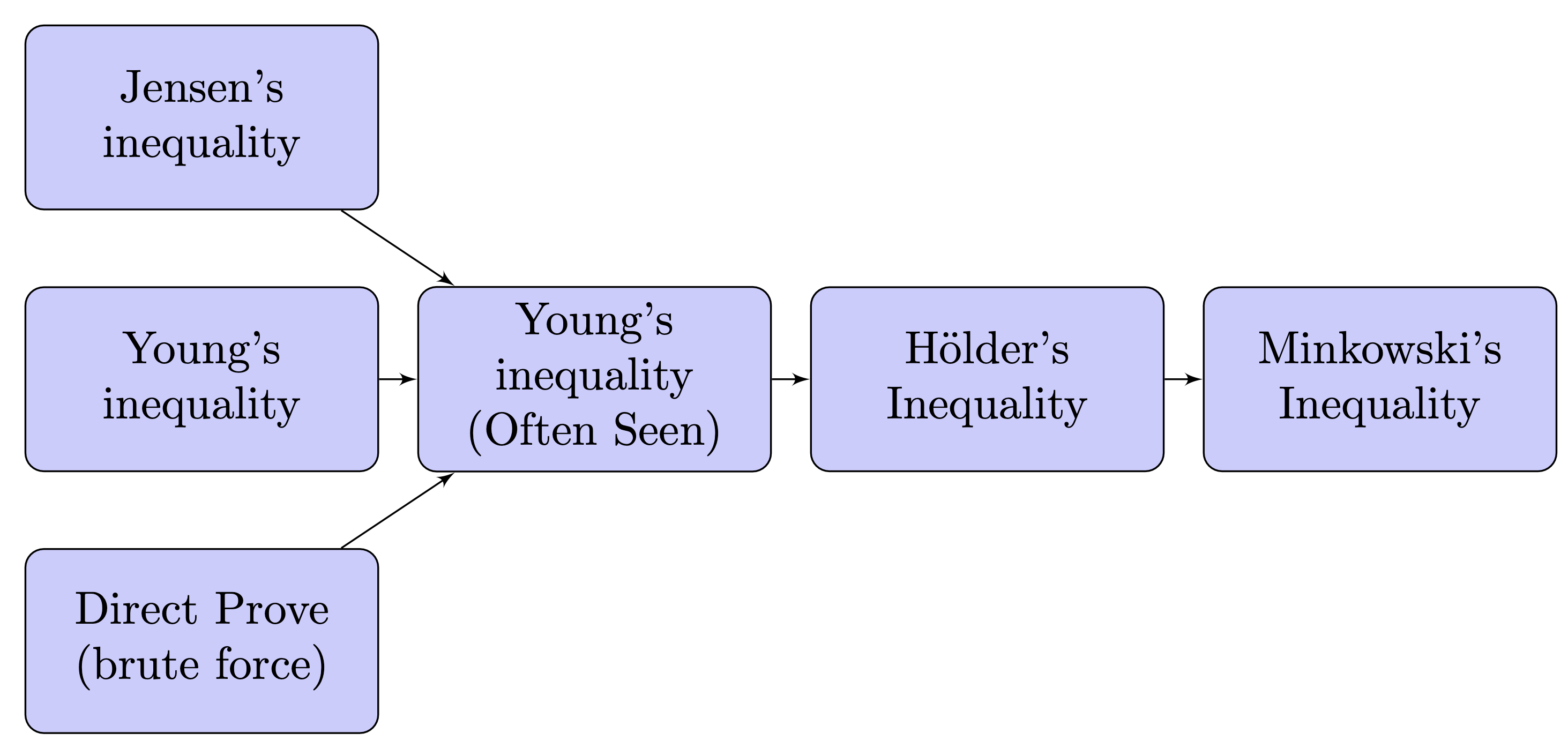
General introduction

In this prove, we will use Young's inequality for products to prove Hölder's inequality, then prove Minkowski inequality.

The proof of Young's inequality for products has been shown in my other blog: Three Ways of Proving Young's inequality for products

Llama:

Young's inequality for products:

\(a, b, p, q \in \Bbb{R}\)

If \(a ≥ 0\) and \(b ≥ 0\), and if \(p > 1\) and \(q > 1\) such that \(\dfrac{1}{p}+\dfrac{1}{q}=1\), then

\[ ab\leq \dfrac{a^{p}}{p}+\dfrac{b^{q}}{q}. \]

Equality holds if and only if \(a^p = b^q\).

---

I met this theorem in Rudin’s PRINCIPLES OF MATHEMATICAL ANALYSIS Exercise 6.10.

Proof of Hölder's inequality

Hölder's inequality (continuous)

\(f, g\) is continuous on \([a, b]\), then

\[ \int ^{b}_{a}\left| f\left( x\right) g\left( x\right) \right| dx\leq \left[ \int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx\right] ^{\dfrac{1}{p}}\left[ \int _{a}^{b}\left| g\left( x\right) \right| ^qdx\right] ^{\dfrac{1}{q}}, \]

where \(p>1\), and \(p\) and \(q\) conjugate (\(\frac{1}{p} + \frac{1}{q} = 1\)).

Equality holds if one of \(f, g\) is zero, or exist \(\lambda\) and \(\mu\) (\(\lambda\mu > 0\)) such that

\[ \lambda\left|f\right|^p = \mu\left|g\right|^q \]

Remark of the theorem

Notice this is actually the inner product of functions. I learned the concept of inner product space in Math 54 - Linear Algebra & Differential Equations at UC Berkeley. Here is a video introducing the concept.

In this way, the equality-hold-condition can be seen as two vectors (functions) are linearly dependent.

The discrete form of Hölder's inequality thus could be see as vectors in \(\Bbb{R}^n\).

Proof of Hölder's inequality (continuous)

Let

\[ \begin{aligned}A=\dfrac{\left| f\left( x\right) \right| }{\left( \int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx\right) ^{\dfrac{1}{p}}}\\ B=\dfrac{\left| g\left( x\right) \right| }{\left( \int _{a}^{b}\left| g\left( x\right) \right| ^{q}dx\right) ^{\dfrac{1}{q}}}\end{aligned} \]

We will first see \(AB ≤ \dfrac{A^{p}}{p}+\dfrac{B^{q}}{q}\), then we integral both side to get right side (\(\dfrac{A^{p}}{p}+\dfrac{B^{q}}{q}\)) be \(1\), then we see the relationship between the denominator and numerator.

We have

\[ \begin{aligned} AB &= \dfrac{\left| f\left( x\right) \right| \left| g\left( x\right) \right| }{\left( \int _{a}^{b}|f\left( x\right) | ^{p}dx\right) ^{\dfrac{1}{p}}\left( \int _{a}^{b}\left| g\left( x\right) \right| ^{q}dx\right)^{\dfrac{1}{q}}} \\ &\leq \dfrac{A^{p}}{p}+\dfrac{B^{q}}{q} \\ &= \dfrac{1}{p}\cdot \dfrac{\left| f\left( x\right) \right| ^{p}}{\int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx}+\dfrac{1}{q}\cdot \dfrac{\left| g\left( x\right) \right| ^{q}}{\int _{a}^{b}\left| g\left( x\right) \right| ^{q}dx} \end{aligned} \]

Rewrite in a clean way:

\[ \dfrac{\left| f\left( x\right) \right| \left| g\left( x\right) \right| }{\left( \int _{a}^{b}|f\left( x\right) | ^{p}dx\right) ^{\dfrac{1}{p}}\left( \int _{a}^{b}\left| g\left( x\right) \right| ^{q}dx\right)^{\dfrac{1}{q}}} \le \dfrac{1}{p}\cdot \dfrac{\left| f\left( x\right) \right| ^{p}}{\int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx}+\dfrac{1}{q}\cdot \dfrac{\left| g\left( x\right) \right| ^{q}}{\int _{a}^{b}\left| g\left( x\right) \right| ^{q}dx} \]

We integrate both side and get

\[ \begin{aligned} \int ^{b}_{a}ABdx &=\int _{a}^{b}\dfrac{ |f\left( x\right) \left| \right| g\left( x\right) | }{\left( \int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx\right) ^{\dfrac{1}{p}}\left( \int _{a}^{b}|g(x)| ^{q}dx\right) ^{\dfrac{1}{q}}}dx \\ &=\dfrac{ \int _{a}^{b}|f\left( x\right) \left| \right| g\left( x\right) | dx}{\left( \int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx\right) ^{\dfrac{1}{p}}\left( \int _{a}^{b}|g(x)| ^{q}dx\right) ^{\dfrac{1}{q}}} \\ &\leq \int _{a}^{b}\dfrac{1}{p}\cdot \dfrac{\left| f\left( x\right) \right| ^{p}}{ \int ^{b}_{a}| f\left( x\right)|^{p}dx}dx+\int _{a}^{b}\dfrac{1}{q}\cdot\dfrac{\left| g\left( x\right) \right| ^{q}}{\int _{a}^{b}\left| g\left( x\right) \right| ^{q}dx}dx \\ &=\dfrac{1}{p}\int _{a}^{b}\dfrac{\left| f\left( x\right) \right| ^{p}}{\int ^{b}_{a}\left| f\left( x\right) \right| ^{p}dx}dx+\dfrac{1}{q}\int _{a}^{b}\dfrac{\left| g\left( x\right) \right| ^{q}}{\int _{a}^{b}\left| g\left( x\right) \right| ^{q}dx}dx \\ &=\dfrac{1}{p}\cdot \dfrac{\int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx}{\int ^{b}_{a}\left| f\left( x\right) \right| ^{p}dx}+\dfrac{1}{q}\cdot \dfrac{\int _{a}^{b}\left| g\left( x\right) \right| ^{q}dx}{\int _{a}^{b}\left| g\left( x\right) \right| ^{q}dx}\\ &=\dfrac{1}{p}+\dfrac{1}{q}\\ &=1 \end{aligned} \]

Note that \(\left( \int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx\right) ^{\dfrac{1}{p}}\)and \(\left( \int _{a}^{b}\left| g\left( x\right) \right| ^{q}dx\right) ^{\dfrac{1}{q}}\) are both constant, thus when integrate over them, they remain the same.

Rewrite in a clean way:

\[ \begin{aligned} \dfrac{ \int _{a}^{b}|f\left( x\right) \left| \right| g\left( x\right) | dx}{\left( \int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx\right) ^{\dfrac{1}{p}}\left( \int _{a}^{b}|g(x)| ^{q}dx\right) ^{\dfrac{1}{q}}} &\leq1 \\ \int _{a}^{b}|f\left( x\right) \left| \right| g\left( x\right) | dx &\leq \left( \int _{a}^{b}\left| f\left( x\right) \right| ^{p}dx\right) ^{\dfrac{1}{p}}\left( \int _{a}^{b}|g(x)| ^{q}dx\right) ^{\dfrac{1}{q}} \end{aligned} \]

By this, we proved the theorem.

Proof of Hölder's Inequality (discrete)

Consider two sequences \((\mathbf{a} = (a_1, a_2, ..., a_n))\) and \((\mathbf{b} = (b_1, b_2, ..., b_n))\), and let \(p, q > 1\) with \(\frac{1}{p} + \frac{1}{q} = 1\). We want to show that

\[ \sum_{i=1}^{n} a_i b_i \leq \left( \sum_{i=1}^{n} a_i^p \right)^{\frac{1}{p}} \left( \sum_{i=1}^{n} b_i^q \right)^{\frac{1}{q}}. \]

Define the sequences \(A_i\) and \(B_i\) as follows:

\[ A_i = \frac{a_i}{\left( \sum_{i=1}^{n} a_i^p \right)^{\frac{1}{p}}}, \quad B_i = \frac{b_i}{\left( \sum_{i=1}^{n} b_i^q \right)^{\frac{1}{q}}}, \quad i=1,2,...,n. \]

From Young's inequality, we have \(a_i b_i \leq \frac{1}{p} a_i^p + \frac{1}{q} b_i^q\), or in terms of \(A_i\) and \(B_i\):

\[ A_i B_i \leq \frac{1}{p} A_i^p + \frac{1}{q} B_i^q, \quad i=1,2,...,n. \]

Summing over all \(i\), we get

\[ \sum_{i=1}^{n} A_i B_i \leq \sum_{i=1}^{n} \left( \frac{1}{p} A_i^p + \frac{1}{q} B_i^q \right) = \frac{1}{p} \sum_{i=1}^{n} A_i^p + \frac{1}{q} \sum_{i=1}^{n} B_i^q. \]

Since the right-hand side equals \(\frac{1}{p} + \frac{1}{q} = 1\), we have

\[ \sum_{i=1}^{n} a_i b_i = \left( \sum_{i=1}^{n} a_i^p \right)^{\frac{1}{p}} \left( \sum_{i=1}^{n} b_i^q \right)^{\frac{1}{q}} \sum_{i=1}^{n} A_i B_i \leq \left( \sum_{i=1}^{n} a_i^p \right)^{\frac{1}{p}} \left( \sum_{i=1}^{n} b_i^q \right)^{\frac{1}{q}}. \]

This concludes the proof of Hölder's inequality in its discrete form.

Connection to the Cauchy-Schwarz Inequality

Note that for \(p = q = 2\), Hölder's inequality reduces to the well-known Cauchy-Schwarz inequality:

\[ (a, b)^2 \leq (a, a)(b, b) \Rightarrow (a, b) \leq \sqrt{(a, a)(b, b)}. \]

The discrete version of Hölder's inequality is thus a generalization of the Cauchy-Schwarz inequality to \(\Bbb{R}^n\).

Proof of Minkowski inequality

Minkowski inequality (continuous)

Let \(f, g\) be functions on the interval \([a, b]\), and let \(p > 1\). Minkowski's inequality states that

\[ \left( \int_{a}^{b} |f(x) + g(x)|^p dx \right)^{\frac{1}{p}} \leq \left( \int_{a}^{b} |f(x)|^p dx \right)^{\frac{1}{p}} + \left( \int_{a}^{b} |g(x)|^p dx \right)^{\frac{1}{p}}. \]

where \(p>1\). Equality holds iff there exist \(\lambda ≥ 0\) such that \(f = \lambda g\) or \(g = \lambda f\)

Proof of Minkowski inequality (continuous form)

The proof begins with the triangle inequality:

\[ \begin{aligned} \int_{a}^{b} |f(x) + g(x)|^p dx &= \int_{a}^{b} |f(x) + g(x)|^{p-1}|f(x) + g(x)| dx \\ &\leq \int_{a}^{b} |f(x) + g(x)|^{p-1}|f(x)| dx + \int_{a}^{b} |f(x) + g(x)|^{p-1}|g(x)| dx \end{aligned} \]

Apply Hölder's inequality to the right-hand side:

One of them is

\[ \int_{a}^{b} |f(x) + g(x)|^{p-1}|f(x)| dx \leq \left[\int_{a}^{b} |f(x) + g(x)|^p dx \right]^{\frac{p-1}{p}} \left\{\int_{a}^{b} |f(x)|^{p}dx\right\}^{\frac{1}{p}} \]

Thus

\[ \int_{a}^{b} |f(x) + g(x)|^{p-1}|f(x)| dx + \int_{a}^{b} |f(x) + g(x)|^{p-1}|g(x)| dx \\ \leq \left[\int_{a}^{b} |f(x) + g(x)|^p dx \right]^{\frac{p-1}{p}} \left\{\left[\int_{a}^{b} |f(x)|^{p}dx\right]^{\frac{1}{p}} + \left[\int_{a}^{b} |g(x)|^{p}dx\right]^{\frac{1}{p}}\right\} \]

Divide \(\left[\int_{a}^{b} |f(x) + g(x)|^p dx \right]\)to both side of the equation, we got

\[ \left( \int_{a}^{b} |f(x) + g(x)|^p dx \right)^{\frac{1}{p}} \leq \left( \int_{a}^{b} |f(x)|^p dx \right)^{\frac{1}{p}} + \left( \int_{a}^{b} |g(x)|^p dx \right)^{\frac{1}{p}}. \]

This completes the proof of Minkowski's inequality.

Minkowski inequality (discrete)

For sequences \(\mathbf{a} = (a_1, a_2, ..., a_n)\) and \(\mathbf{b} = (b_1, b_2, ..., b_n)\) with \(p > 1\), Minkowski's inequality can be expressed as:

\[ \left( \sum_{i=1}^{n} |a_i + b_i|^p \right)^{\frac{1}{p}} \leq \left( \sum_{i=1}^{n} |a_i|^p \right)^{\frac{1}{p}} + \left( \sum_{i=1}^{n} |b_i|^p \right)^{\frac{1}{p}}. \]

where \(p>1\). Equality holds iff there exist \(\lambda ≥ 0\) such that \(\mathbf{a} = \lambda \mathbf{b}\) or \(\mathbf{b} = \lambda \mathbf{a}\)

Proof of Minkowski inequality (discrete form)

\[ \left( \sum_{i=1}^{n} |a_i + b_i|^p \right)^{\frac{1}{p}} \leq \left( \sum_{i=1}^{n} |a_i|^p \right)^{\frac{1}{p}} + \left( \sum_{i=1}^{n} |b_i|^p \right)^{\frac{1}{p}}. \]

The proof utilizes the triangle inequality in the following way:

\[ \sum_{i=1}^{n} |a_i + b_i|^p = \sum_{i=1}^{n} |a_i + b_i|^{p-1}|a_i + b_i|. \]

By applying the triangle inequality, of

\[ |a_i + b_i|^{p-1}|a_i + b_i| \leq |a_i + b_i|^{p-1}|a_i| + |a_i + b_i|^{p-1}|b_i|. \]

We get

\[ \sum_{i=1}^{n} |a_i + b_i|^p = \sum_{i=1}^{n} |a_i + b_i|^{p-1}|a_i + b_i| \leq \sum_{i=1}^{n} |a_i + b_i|^{p-1}|a_i| + \sum_{i=1}^{n} |a_i + b_i|^{p-1}|b_i| \]

From Hölder's inequality we get

\[ \sum_{i=1}^{n} |a_i + b_i|^{p-1}|a_i| + \sum_{i=1}^{n} |a_i + b_i|^{p-1}|b_i| \leq \left(\sum_{i=1}^{n} |a_i + b_i|^{p}\right)^{\frac{p-1}{p}} \left[ \left(\sum_{i=1}^{n} |a_i|^p\right)^{\frac{1}{p}} + \left(\sum_{i=1}^{n} |b_i|^p\right)^{\frac{1}{p}}\right] \]

Dividing both sides by \(\left( \sum_{i=1}^{n} |a_i + b_i|^{p} \right)^{\frac{p-1}{p}}\), we arrive at Minkowski's inequality:

\[ \left( \sum_{i=1}^{n} |a_i + b_i|^p \right)^{\frac{1}{p}} \leq \left( \sum_{i=1}^{n} |a_i|^p \right)^{\frac{1}{p}} + \left( \sum_{i=1}^{n} |b_i|^p \right)^{\frac{1}{p}}. \]

This concludes the proof of the discrete form of Minkowski's inequality.